Creation Corner
Energy of lunar month

How many days made a true month before the Global Flood? How much kinetic energy did the Moon lose to settle into its modern lower (and shorter) orbit? Where did that energy go? That debate has drawn little attention in the lay press. But it forms a small part of a larger debate: did a Global Flood occur at all? What made the “mavericks of the Solar System”? And when did the moon lose its energy?
On May 31, Walter T. Brown of the Center for Scientific Creation revised that part of his Hydroplate Theory that deals with the energy of the month. Today Dr. Brown and I present details on the amount of energy the moon must have lost to drop into its lower orbit. We show the moon lost this energy after several very heavy and fast objects bombarded it. The bombarding objects need not have melted the moon but might have given the moon its present liquid-metal core. And the Bible gives a likely clue to when this happened.
What energy does a body in orbit have?
Sir Isaac Newton worked out how strongly every particle in the universe attracts every other particle. We call this the Law of Gravity:
where M and m represent the masses of the primary and the orbiting body, G represents the Newtonian gravitational constant, and R represents the radial distance between the two bodies.
A body in orbit has a certain orbital energy. By convention, investigators treat this as a negative. It represents the energy one would need to break out of an orbit. A body of mass m orbiting a primary of mass M at semimajor axis a (the best average distance between the two bodies) has this much energy:
A month is the period of a moon, the time to start from one point and come back to the same point. This value is:
So that:
So:
and thus:
How much energy did the moon have to lose?
At least three percent of the earth’s mass escaped from the earth during the Flood event. That mass persists as the “mavericks of the Solar System”: meteoroids, asteroids, comets, and trans-Neptunian objects.
If none of these objects had bombarded the Moon, the Moon would have coasted to a higher orbit with a longer month. Brown calculates the synodic month (the time for the moon to cycle exactly once through its phases) expanded from 30 days to 31.930 days. But today a synodic lunar month has 29.531 days. Furthermore, those days do not last as long as a day lasted before. The ancient Egyptians and Babylonians kept a calendar with a 30-day month and a 360-day year. Today a year has 365.256 days.
So the objects that bombarded the moon, needed to rob it of this much energy to slow it to its modern orbit:
In other words, the moon lost six percent of its orbital energy in the bombardment that followed the breakout of the subcrustal ocean.
(Critical observers will readily see that synodic months differ from sidereal months, the time taken for the moon to return to the same alignment with the stars. But in this first-order approximation, the difference does not matter.)
Does this energy loss present a heat problem?
Critics of this part of the Hydroplate Theory say the moon couldn’t have taken this bombardment without breaking apart.
First, let us calculate an energy budget. To do that, we need the values of G, M, m, and a.
Henry Cavendish measured the gravitational attraction between two objects of known mass at a known distance. From this he calculated G:
In so doing, Cavendish weighed the earth:
The moon has 1.23 percent of the mass of the Earth:
The moon follows a near-circular orbit:
Thus:
The original value was 6.383 percent higher, so the moon lost this much energy:
Brown proposes the moon lost that amount of orbital energy from bombardment. That much bombardment must have transferred heat to the moon, perhaps as much as that 2.417 octillion joules, perhaps more, perhaps less. The efficiency of any particular strike (that is, how much energy went into changing the orbit of the moon instead of wasting as heat) depends on how far the lunar material would compress under that strike. Two octillion four hundred seventeen septillion joules likely represents the worst case.
Two questions, not merely one, need answers:
- Could the moon have absorbed that much heat without melting through-and-through or disintegrating from the impacts? Clearly the moon did neither. It survived intact, with craters and lava flows that reflect the bombardment.
- Does the moon hold an amount of heat today, that one would expect the moon to have after having 5300 years to cool off?
Why 5300 years? Because the Biblical Flood Event took place that long ago. The orbits of the comets (especially Halley and Swift-Tuttle) tell us that.
Evidence for bombardment
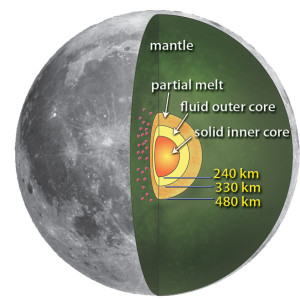
Cutaway of the moon showing the solid-fluid core, partial melt, and mantle, inferred from seismic data from Apollo 14, 15, 16, and 17. Diagram courtesy Renée Weber/NASA
All scientists, conventional or creation-oriented, will stipulate the moon has suffered bombardment. Craters cover the moon’s far side, and to a lesser extent the near side. The near side’s smooth areas, or maria, represent basaltic flows. The moon also has:
- A solid inner core and liquid outer core, similar to those of earth, and
- A number of “mass concentrations” or “mascons,” each associated with one “sea” on the near side of the moon. The five largest lie deep to Oceanus Procellarum and Maria Frigoris, Imbrium, Crisium, and Tranquillitatis. The moon has smaller mascons on the near side, deep to other maria like Sinus Medii (“Central Bay”) and Mare Smythii (Smythe’s Sea). The gravity map on the far side (see below) shows no high-gravity region comparable to a near-side mascon, either in area or in strength.
Six two-man teams landed on the moon during Project Apollo. (A nearly crippling on-board accident forced the crew of Apollo XIII to return to Earth after one pass.) Those crews brought back samples of rock and soil that proved remarkably earth-like. Some held radioactive elements. All these samples came from or near the surface. (See here, here, and here.)
Those who suggest the moon would have melted under the bombardment, might have assumed the moon got hot before it got hit. This cannot be correct. If the age of the moon is 4.5 billion years, the moon might then have been not only molten but vaporized. No: the moon got hot when it got hit, and because it got hit.
The Moon also has an atmosphere, about 10-14 times as thick as that of Earth. Oxygen makes up most of this. Where did that come from? Probably from water that splashed onto the moon, then dissociated into the two elements (hydrogen and oxygen) that make up water. The hydrogen would escape; the heavier oxygen would not. (But this oxygen “atmosphere” cannot stop the meteoroids that bombard the moon to this day.)
Nicholas M. Short, in the Prentice-Hall Planetary Geology textbook, noticed heat flowing out of the moon, faster than anyone predicted. NASA infers this from buried thermocouple arrays that different Apollo teams left at their landing sites. Short mentions specifically Apollo XV (David Scott and James Irwin) and Apollo XVII (Eugene Cernan and Harrison Schmidt, the only PhD geologist ever to fly to the moon). In 1975 Short wrote:
Actual values of heat flow determined on the Moon at the Apollo 15 and 17 landing sites were two and three times higher than…predicted.
And he found this
a somewhat surprising outcome considering the size of the Moon and the assumption that most of its heat energy had been lost.
In 2011, Renée Weber and her team worked out the existence of the inner and outer cores and the partial melt layer surrounding them. The diagram (above right) comes from her paper.
Tim Sharp at Space.com reports one (uncredited) guess for the lunar core temperature: 1600 to 1700 kelvins. The solid inner core contains metals that did not melt at that temperature. The earth has a much hotter core: about 6300 kelvins at the boundary between the inner and outer cores.
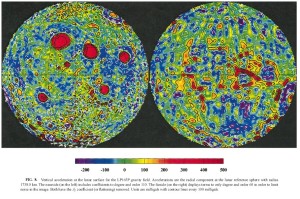
Gravity map of the Moon, by Lunar Prospector. Note the five bright-red objects corresponding to known mascons deep to the five largest lunar maria. The far side (disk right) shows no comparable gravity field. Graphic courtesy NASA.
NASA first discovered the mascons in 1968, while Project Apollo was still running its test missions. Two years ago NASA sent this press release about the mission they called GRAIL (Gravity Recovery And Interior Laboratory; see also here and here). GRAIL used two spacecraft, communicating by laser, to map the mascons precisely. Mission controllers then compared their observations to models of large-object impacts. They concluded: each mascon formed when a heavy object crashed into the Moon.
They also concluded the large objects hit the moon when it was already hot, and hotter than today. But that makes little sense. Each mascon lies deep to a lunar “sea.” The maria all have basaltic floors. This implies a lava flow over a cool surface after the impact. Else why would the surface be any more remarkable over a mascon than, say, on the far side?
Suppose, instead, the mascon impactors, and all the other cratering impactors that fell after them, combined to make the Moon hot? Would that not produce the same observed findings?
When and how did this happen?

Comet Shoemaker-Levy 9, broken up into 21 pieces that are about to rain down on Jupiter. Photo from the Hubble Space Telescope, courtesy of NASA, the European Space Agency, the Space Telescope Science Institute, and investigators H. Weaver and E. Smith of STScI.
Neither Moses nor any of the Annalists (Adam, Noah, Shem/Ham/Japheth, Shem alone, Terah, Isaac, Jacob, and Joseph) he relied on for events happening before he was born, record any apparent “heavenly conflict” or anything a modern scholar might interpret as the bombardment of the moon. The bombardment cannot have happened sooner than the Global Flood. How long after the Flood did it happen?

The planet Jupiter, showing where the fragments of Comet Shoemaker-Levy 9 struck it. Photo by the Hubble Space Telescope, courtesy of NASA and the HST Comet Team.
NASA’s mascon map gives a clue. To understand it, recall a more modern event. In July of 1994, Comet Shoemaker-Levy 9 passed too close to the planet Jupiter. It broke up into twenty-one fragments. These then fell to Jupiter. And incredibly, astronomers could plainly see the spots where the fragments fell. The photo at left shows Jupiter after the impacts. Notice the pattern: beads on a string.
Look again at the near-side disk on the mascon map. Notice the three mascons roughly near Maria Crisium, Frigoris, and Imbrium. Like the Shoemaker-Levy 9 impact sites, they line up like beads on a string. The two other mascons to their south, lie no more than ninety degrees of arc away from this string.
Notice also: the mascon deep to Oceanus Procellarum lies southwest of the mascon for Mare Tranquillitatis. The far side of the moon has one “sea,” Mare Moscoviense, to the southeast as one looks down on the moon from the second Lagrange point, opposite the moon from the earth.
These mascons sit about where they would sit, if they began as the fragments of a larger object that passed inside the moon’s Roche limit and broke up. (The Roche limit is as close as an object can get to a larger object before tidal forces will break the smaller object apart.) Perhaps the object broke into two objects, which each broke apart again to rain down on the moon, hard enough to melt some of the moon’s substance and make it flow like lava. (Brown took caution in his approach to this part of the problem. The crossover depth of the moon would limit the amount of lava that would flow. Brown tentatively concludes the crossover depth is at or near the boundary of the moon’s liquid outer core. So any magma that formed from the impact of a future mascon would bubble up to flow as lava.)
But where could this object have come from? Any object large enough to break up to form more than five giant impactors, must be an asteroid. Asteroids, according to the Hydroplate Theory, formed after the Global Flood. Their raw material escaped the earth in the breakout of the “fountains of the great deep,” as Shem, Ham, and Japheth described them (Genesis chapter 7).
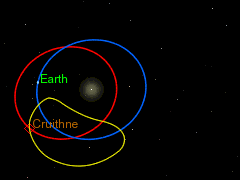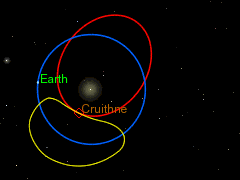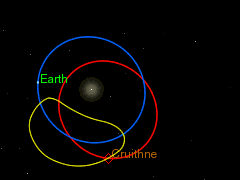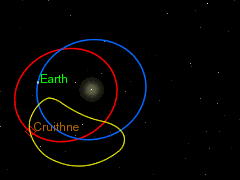
Asteroid 3753 Cruithne and its apparent path from the perspective of an earth-bound observer. Graphic by User Jecowa on Wikimedia Commons, using the Celestia electronic-orrery program. CC BY-SA 3.0 Unported License.
Near-earth asteroids pass close to earth more often than our highly technological civilization might find comfortable. In addition, the earth has companion asteroids. These follow orbits that track the earth closely and have a sidereal period of about one earth year. Asteroid 3753 Cruithne, famous for its “horseshoe orbit,” is the prize example. Cruithne has a sidereal period of one year but a synodic period (time between closest approaches to earth) period of more than 380 years. Nor is 3753 Cruithne the only such asteroid. Earth has several.
Asteroid 3753 Cruithne is about five kilometers in diameter, thus 2.5 kilometers in radius. This would give it a volume of about 65 cubic kilometers. The moon has a density of 3100 kilograms per cubic meter, which would be 3.1 trillion kilograms per cubic kilometer. So perhaps 3753 Cruithne has a mass of two hundred trillion kilograms.

Creater Earhart, named for Amelia Earhart (inset), deep to Mare Serenitatis. Photo courtesy Arizona State University. Hosted by the National Geographic Society.
Now consider a companion asteroid at least as large as Cruithne, or larger. Much larger. Call it Cruithne’s Big Brother, for lack of a better name. Imagine Big Brother in a horseshoe orbit, having a synodic period of about 400 years, like that of Cruithne. Now imagine Big Brother in an orbit in or near the plane of the ecliptic, instead of inclined about 19 degrees from it, like the orbit of Cruithne. This object, at a time of closest approach, passes through the Roche limit of the moon. It breaks up. Its fragments slam into the moon and turn it into the pockmarked world we know. (Three months ago NASA reported at least one crater lies buried in basalt on the floor of Mare Serenitatis. Clearly the seas formed after some of the craters did.)
But when did this happen? Again, one of the Genesis Annalists should have recorded it. And perhaps one did. Which one? Joseph, son of Israel, former steward to Potiphar, former “trusty” and almost a deputy warden at the House of the Curve (the Egyptian equivalent of Alcatraz, dug out of a sheer cliff at a curve of the Nile), and finally grand vizier of Egypt, during one of the most disastrous periods of the history of Egypt and the ancient Near East: the Biblical Famine.
In 1783, Mount Laki in Ireland erupted, with 9,000 casualties. It threw up a cloud of dust that disrupted the weather as far south as Egypt. Scientists at Rutgers University concluded: that dust cloud reduced the flow of the Nile, causing a famine as the annual Inundations fell below acceptable levels.
No scholar has yet traced the event that triggered the Biblical Famine: seven years of bounty, then seven years in which the Inundations failed. Now consider: suppose one of the fragments of Cruithne’s Big Brother fell, not to the moon, but to the earth? The Laki example clearly shows a big-enough meteor could kick up enough dust to affect the weather at the sources of the Nile. (The Nile begins as the union of two rivers, the White Nile and the Blue Nile.) So for seven years, the Nile fails to flood its bottom lands. Had not Pharaoh Djoser (the most likely candidate) thought to have anyone store enough food to get through that drought, the Egyptian state would not have survived. But of course the Bible tells us Djoser had two disturbing dreams of hunger wiping out plenty. Then his chief cupbearer suddenly said in effect, “Hey, I just remembered! A Hebrew trusty, down in that Hole where you sent me, predicted I would be back in your good graces in three days. Maybe you should talk to him!” With the result you know.
Let the still-skeptical reader consider this: none of the Genesis Annalists, except only Shem, Ham and Japheth while they kept the Log of Noah’s Ark, recorded dates with any degree of precision. Instead, for instance, Jacob records that “Reuben went, in the days of the wheat harvest, found mandrakes [Mandragora officinarum or some such species] growing in the field, and brought them to his mother Leah.” In sharp contrast, Moses records the precise date of the Passover: “in the first month, in the fourteenth day of the month.” He then records:
Now the time that the sons of Israel lived in Egypt was four hundred thirty years. And at the end of the four hundred thirty years, to the very day, all the hosts of YHWH went out from the land of Egypt. (Exodus 12:40-41, NASB)
Four hundred thirty years before, Jacob entered Egypt (Genesis chapter 46) with all his family who didn’t already live there. This happened after the Biblical Famine. Moses obviously could calculate the time as precisely as we can calculate it today. This strongly suggests the event that robbed the moon of its energy, and set the synodic month to its modern length, happened before Jacob entered Egypt but after Jacob left his father-in-law in Padan-Aram (ancient Syria) and returned to Canaan. The Biblical Famine is the most likely such event. We can now see it as an incidental casualty of the great bombardment of the moon.
Why didn’t anyone see that bombardment? Because it likely happened during or within days of the dark of the moon. Even such high-energy impacts, enough to produce lava flows, might not have produced flashes of light anyone could see that close to the sun. (And of course, nighttime observers could see nothing at all.)
Conclusion
Dr. Brown and this correspondent have examined the evidence of the last half century. This includes the test missions of Project Apollo (VIII and X), the six successful sample-and-return missions (XI, XII, XIV, XV, XVI, and XVII), and more recent, higher-precision measurements from robotic missions (GRAIL, Lunar Prospector, and others). We conclude the moon suffered a high-energy bombardment from large amounts of water, mud, and rocks, varying in size from microscopic dust particles to the great impactors that persist as the mascons. These large impactors fell mainly on the leading face of the moon. They unbalanced the distribution of mass and thus turned that leading face toward the earth permanently in tidal lock. Before the tidal lock happened, innumerable impactors fell on the moon, predominantly during its crescent phases.
The material for these impactors first came from the breakout of a subcrustal ocean under tremendous pressure. Much of this material formed companion asteroids that fell into “horseshoe orbits” around the earth (actually around the sun but apparently around the earth). At least one of these companion asteroids drifted inside the Roche limit of the moon and broke up into several large fragments. These fell to the moon, started the lava flows that formed the maria, and also robbed the moon of about six percent of the orbital energy it once had. This dropped it into a lower orbit with a shorter period. But at least one fragment fell to earth. This high-energy impact threw up enough dust to disrupt the weather at the sources of the Nile River. This catastrophic weather change provoked the Biblical Famine, which only Divine warning stopped short of the destruction of the civilizations of the ancient Near East.
The ancient Hebrews reckoned their months by the rising and falling of the Moon and the ripening of the barley in Jerusalem. This hint about the intercalary month of Adar sheni suggests the Israelites “threw in” this month during the Exodus (1491-1451 BC). They likely threw it in earlier, since they first entered Egypt 430 years before that event.
The same impacts that dropped the moon into a lower and shorter orbit, also gave the moon its heat. We do not have precise-enough projections of how much heat the moon is radiating away. More-precise readings of the lunar heat flux, enough to produce a decay curve, and better modeling of the heat release from impacts from objects of different masses, might tell us over what period the slow-down of the moon occurred, and how hot the moon could have gotten, from a cold “start.” in a series of impacts starting about fifty-three hundred years before the present.
Terry A. Hurlbut has been a student of politics, philosophy, and science for more than 35 years. He is a graduate of Yale College and has served as a physician-level laboratory administrator in a 250-bed community hospital. He also is a serious student of the Bible, is conversant in its two primary original languages, and has followed the creation-science movement closely since 1993.
-

 Executive2 days ago
Executive2 days agoJanuary 6 case comes down to selective prosecution
-

 Executive1 day ago
Executive1 day agoBiden ballot woes continue
-

 News2 days ago
News2 days agoRolling the Dice on Republicans: Has the Right Become Delusional?
-
 Civilization1 day ago
Civilization1 day agoPresident Biden Must Not Encourage Illegal Mass Migration From Haiti
-

 Executive2 days ago
Executive2 days agoWhy Fatal Police Shootings Aren’t Declining: Some Uncomfortable Facts
-

 Guest Columns1 day ago
Guest Columns1 day agoWhat Was Won in No Labels’ Crusade
-

 Civilization2 days ago
Civilization2 days agoBiology, the Supreme Court, and truth
-

 Entertainment Today2 days ago
Entertainment Today2 days agoWaste of the Day: Throwback Thursday: Millions Went To Video Game ‘Research’















Katherine Lester liked this on Facebook.
Johnny Helbo liked this on Facebook.
Margaret Mulvihill liked this on Facebook.
Ricki Ricardo liked this on Facebook.
walter brown is a creationist,thats all you need to know to discount his nonsense.
All right, so how do you explain how the moon turned a face to the earth, and where the bombarding objects have come from?
Yeah, absolute nonsense, especially considering his crazy predictions are being consistently confirmed. Can’t have that.
they are not
Okay then.
walter brown is a looney tune
Well-poisoning, much? Here you have a textbook example: before someone even begins to speak, someone says, “But he advocates such-a-thing, which makes no sense.” And that includes another logical fallacy: begging the question. In this case: why doesn’t it make sense?
Chris it would appear you have taken that honor..since you seem to be the odd ball out here.
“The nitrogen in our DNA, the calcium in our teeth, the iron in our blood, the carbon in our apple pies were made in the interiors of collapsing stars. We are made of starstuff.”
― Carl Sagan, Cosmos
Johnny Helbo, I see you have read Brown’s work and have seen the predictions he has made over the years, predictions that have worked out.
Carl Sagan has no foundation for those statements. For he still must explain how colliding dust clouds could come together and accrete, then how life arose from some sort of biological ylem. He can do neither. I have not seen the authority who can.
The biggest prediction being water under the major mountain ranges.
just because someone makes a comment doesn’t mean they haven’t looked into the topic in depth. you conclude that the comment is meaningless. you are wrong.
what predictions has brown made that worked out? none.
Haha Chris maybe you should read his book before commenting further as you are just coming across as uninformed at this stage. Walter Brown has made several stunning predictions that have been confirmed through modern science.
i pointed out carl sagan’s quote to hi-light that we know where minerals etc came from.
read his nonsense? i have . no one has yet stated what these “stunning” predictions are .
Why..because Sagan said so??
He did..clearly you have not read his work or you would know that.
i note you can’t say what these predictions actually are can you? it seems that not only brown confused and inarticulate but so are you.
I will not go the insult route with you..I just mentioned one of his predictions..that water would be found under major mountain ranges. It has been confirmed in several ways..GPR, being one of those methods.
you mean you just mentioned it now. whats so stunning about that? there are plenty of water tables.
I actually went to Walt’s home in Phoenix to discuss his theory with him. I’ve studied it for several years, and I think he’s bang on. I must be stupid, right Chris?
i don’t think YOU understand browns sill hydroplate theory.
The biggest prediction being water under the major mountain ranges.
Like · 1 · 19 mins
yes you are! i would ask what brown smokes or ingests.
It was also warm and salty also predicted by Brown.
I’m all for a respectful debate, I simply will not engage you if all you are going to do is tell everyone else they are stupid. If you want a debate than try having some class, and propagate some scientific evidence which refutes Brown’s claims.
Johnny, I have been studying it for the past seven months, I find it to be completely sound; and have seen no successful argument to refute its validity.
oh,excuse me,you made the statement thta you were stupid ,i agreed with you. typical of those who can’t discuss. you try to blame the other person you made a derogatory comment to as the source of the comment. FAIL!
and what scientific proof have you provided of browns claims? you can’t even provide any evidence of his “predictions”.
Walt Brown is never shy about publishing his predictions. He’s missed only one so far. Who else can make the same claim?
studying what? it is a ridiculous idea. and ,though brown claims to be a creationist creationists don’t agree with him either. and neither does the bible.
First that was Johnny, not me. Secondly, Browns book is full of very scientific references and those who validate his claims, therefore it is you who have provided nothing to refute his claims and it is you who is responsible for the burden of proof.
shy??? where? more like WRONG! and unscientific. you still haven’t provided his predictions
They are all in the book, all you have to do is read it..
browns book is bullshit!
Actually the Bible is in better agreement with his theories than with those of any other single investigator. As to those “other guys,” they have the same problem you have: they can’t propose anything better. He’s competing with someone who invokes miracles as part of the Flood event, and with another theorist who sees the word translated as “firmament” and makes too much of it.
Your continued well-poisoning is getting old fast.
propose anything better? brown is a mechanical engineer. he is not a scientist nor is he a geologist
you continued belief in stupid is getting worse. do you take fluoide pills 3x’s a day?
He’s familiar with the lingo. But he rejects The Narrative about billions of years.
wow! he is a moron is what he is. it takes billions of yrs for things to form. time is what is needed. it takes TIME to make things.
I think you mean fluoride?
That is what you believe, what we actually observe is that it does not take time, it takes water and lots of it.
what takes water?
Guilty. Shall I take it back? Sedimentary layers are deposited in water, and sorted by it. Time erodes and flattens. There should be no mountains after several million years. This is what is observed. They don’t just ‘grow’. There needs to be a cause for the effect.
i guess you never heard of volcanoes have you? or plate tectonics.
“Brown’s model is overwhelmingly rejected by conventional scientists, since it conflicts with extensive geologic evidence that the earth is over 4.5 billion years old, as well as many specific lines of geologic evidence (Morton, 2003). In view of the latter, even many creationists have rejected or strongly questioned the model. One of its serious problems is the need for the proposed water reservoir to be totally sealed within the crust. This precludes any significant earthquakes, meteorite impacts, or even fissures and cracks in the crust anywhere on entire earth, even though such phenomena are well evidenced throughout the geologic record. As Christopher Sharp (2005) notes, Brown gives no satisfactory explanation as to how so much water could be trapped below the upper layer of rock, and how that upper layer remained impervious until the flood. As demonstrated by Glenn Morton (a geologist and former creationist), the earth’s surface would also have to be almost perfectly smooth–lacking any mountains or even hills– or the crust would buckle in places and release the waters (Morton, 2003). Yet according to the Bible (Genesis 49:26) there were mountains before the Flood, which Brown accepts and even shows in a diagram (fig. 56) on his website. Another major problem is the immense heat that would be generated during the proposed cataclysmic eruption (Castagnoli, 2009; Morton, 2003; Sharp, 2005). The magnitude of such heat would have literally boiled the oceans and poached all animals and humans, including the inhabitants of Noah’s ark. Appealing to supposed experiments with “supercritical” water, Brown claims the heat would be insignificant, but the calculations of critics with appear to effectively demonstrate that the heat would indeed be more than lethal.”
Volcanic activity, like the molten core of the earth, has its origin in the gravitational settling that followed the Flood event. And Brown effectively cleans the clock of the plate-tectonics theorists in a very simple synoptic table. That table clearly shows the Hydroplate Theory readily explains all the details that demand explanation. And for plate tectonics, those same details are total deal-killers.
What evidence do you cite that “the earth is over 4.5 billion years old”? May I remind you to check out his chapter on the Origins of Earth’s Radioactivity. I would surmise you cite the radioactive dates of rocks deeper than the Cambrian Layer. Brown clearly shows all radioactive materials had their origin in the Flood event. So they absolutely, positively cannot serve as a reliable clock for the earth.
LMAO!!!!!!!!!!!!!!!!!!!!!!!As demonstrated by Meert (2002), “Radioactive decay at a rate fast enough to permit a young earth would have produced enough heat to melt the earth.”
Not if the metals assumed to be “daughter nuclides” were never radiogenic. Radiometric dating assumes–without warrant–that the starting amount of daughter nuclide is zero. Brown, and I, assert it wasn’t zero. And neither you nor any of the authorities you cite can prove it was zero.
Hasn’t carbon14 been found in all sedimentary layers, diamonds, coal, oil, etc. ? Wouldn’t be there at all if older than 80,000 years.
Carbon-14, as long as anyone mentioned that, is a cluster-decay product. Everyone should read the Radioactivity chapter in full and in detail. The process by which we got radioactive materials went something like this: heavy but still-stable elements fused, in the highly-charged environment from magnitude-10-to-12 earthquakes acting on buried quartz, to form super-heavy elements. These then split to form the abundances of uranium and thorium we have today, plus many other elements in the decay series. Carbon-14 was a common product of this activity. And the dumping of so much carbon-14 into the biosphere, coupled with the sequestration of carbon-14 as “fossil fuels,” combined to shorten the life spans of man and animals by ninety percent in eleven generations of man over the next thousand years.
These magnitude 10-12 earthquakes produced the phenomenon known as Z-pinch?
Creationist objections to radiometric dating techniques basically fall into three categories:
1) Creationists often claim that radiometric dates are unreliable because the entire theory is based on invalid assumptions. We’ve already seen that this doesn’t hold up under examination. The assumptions that are used in radiometric dating techniques are perfectly justified given current physics.
2) Creationist geologists compile long lists of dates obtained by radiometric techniques that deviate widely from the normally accepted values. Creationist geologist John Woodmorappe is the best known of the creationists who attempt this approach. He’s compiled a list of several hundred radiometric dates that are widely divergent from the values accepted by conventional geology. Based on this, he claims that radiometric dating methods don’t produce consistent results, that geologists conceal radiometric dates which don’t match what’s expected, and that therefore the whole methodology of radiometric dating is worthless.
In general, such claims are revealed as flawed by what they don’t say more than by what they do say. In an article for the creationist journal Creation Science Research Quarterly, Woodmorappe listed 350-odd aberrant dates, and claimed that there are many, many more. What he did not say is that those 350 were winnowed out of tens of thousands of radiometric dates which do give more reasonable results. If we run dating tests on 500 samples and 350 (70% of the total tests) are scattered all over the place, with only a few anywhere near the expected values, then we clearly have a serious problem. But if we run dating tests on 10,000 samples and get 350 aberrant results (3.5% of the total), that could easily be simple experimental error. If we test fifty samples from the same rock formation and we get 2 ages of 1 million years, 2 ages of 500 million years, and 46 ages all clustered around 175 million years, it’s not a great leap of logic to conclude that the 4 aberrant results were in error, and the 46 clustered results are probably correct.
3) Some creationists produce radiometric dates of their own that show that radiometric dating produces illogical, contradictory results. A classic example of this tactic is a claim by creationist geologist Steve Austin that rocks taken from Recent lava flows on the Uinkaret Plateau at the top of the Grand Canyon produce older dates than rocks taken from the bottom of the canyon, when both samples are dated using the Rb87/Sr87 isochron method. This appears to be a serious blow against the Rb/Sr isochron technique, but in his article “A Criticism of ICR’s Grand Canyon Dating Project,” Chris Stassen points out that Austin made a critical error in his work. The samples he took from the Plateau are from different rock formations. For any type of radiometric dating to work properly, all samples must come from the same formation. So it’s not surprising that Austin’s results make no sense. “—
Further, radiometric dates can be checked by other dating techniques. When they are, the dates almost always agree within the range of expected error. In cases where the dates don’t agree, it’s always been found that some natural factor was present which selectively affected one or the other dating method being used.
Creationists are forced to challenge radiometric dating because it stands as the most powerful and most damning evidence against their idea of a young Earth. But in the end, they are reduced to saying that “radiometric dating must be wrong, because we know it happened this way.” And that is not a scientific position. If theory says it happened this way and evidence says it happened that way, theory must be revised to fit the evidence. Creationists won’t do that. That reveals creation ‘science’ to be a sham, and not any kind of science at all.
As an engineer, Brown has a leg up on ‘geologists’ in that he understands the forces involved, whether that be the hydro plate theory, or plate tectonics. There’s a reason geologists don’t build bridges.
Further, radiometric dates can be checked by other dating techniques. When they are, the dates almost always agree within the range of expected error. In cases where the dates don’t agree, it’s always been found that some natural factor was present which selectively affected one or the other dating method being used.
Creationists are forced to challenge radiometric dating because it stands as the most powerful and most damning evidence against their idea of a young Earth. But in the end, they are reduced to saying that “radiometric dating must be wrong, because we know it happened this way.” And that is not a scientific position. If theory says it happened this way and evidence says it happened that way, theory must be revised to fit the evidence. Creationists won’t do that. That reveals creation ‘science’ to be a sham, and not any kind of science at all.
wrong. as a mechanical engineer he is way out of his league
The excess argon finding by Austin, and the dating conflict finding by Snelling, I consider absolute deal-killer damning evidence against radiometric dating. And you know that must be the case. When a ten-year-old lava dome yields five different apparent dates varying from half a million to two point eight million years, something is wrong. Something. Is. Very. Wrong.
Not to mention, okay I will, the helium found in zircon crystals. It argues that they are between 4-6 thousand years old. It leaks out at a known rate, thereby nullifying the ridiculously high numbers evolutionists cling to.
actually it appears to us to be fixed
It didn’t always appear to be fixed. It didn’t start that way.
no it didn’t.
We agree on that.
okay
Andrew Snelling did his own independent experiment with known- date lava flows, although amazingly young, a dating laboratory in Boston placed the samples at millions of years old. Several researchers have shown similar failures with known-date objects. One such experiment showed a clay pot with a known date of origin of 300 years, to be 1.2 million years old. link to creation.com
snelling is a fool.
Ahh, I see. So everyone who doesn’t support your silly worldview that defies all that we truly observe is incompetent.. got it.
Your opinion notwithstanding, Andrew Snelling is a brilliant researcher, but that was not even necessary to conduct the experiment he did,any average Joe could have done it.
The really interesting part is the result of this experiment which was conducted by a prestigious laboratory in Boston. The result was..radio isotope dating methods are inaccurate and unreliable.
This will probably take several posts to comment on fully.
“Today Dr. Brown and I present details on the amount of energy the moon must have lost to drop into its lower orbit.” True enough, and an improvement on Dr. Brown’s erroneous previous calculation described in your Aug 3 2014 post where you or he neglected to calculate the new orbital period immediately post-Flood, and so got a value of 4.6% for the same starting assumptions instead of the 6.3% you now claim.
“We show the moon lost this energy after several very heavy and fast objects bombarded it.” No, you assert it without showing it at all. Where are the calculations to show how your proposed massive, fast objects slowed the Moon down? How much kinetic energy from the impactors would have been converted to heat? As an example, the authors of the _Science_ paper that you linked to stated that their model of mascon formation involved impactors 50 km in diameter, with the density of dunite (3.25 g/cc) striking vertically at 15 km/s. My quick order-of-magnitude calculation shows that this would have changed the velocity of the Moon by 0.00004 m/s, with 99.99997% of the kinetic energy of the impactor going into heat; thus the immediate formation of a pool of 1800 K molten rock 200 km across and 100 km deep from each impact. Five, or ten, or a hundred such impacts, even if striking at the best possible time and angle, would not rob the Moon of 6% of its orbital energy. As I recall, the total delta-v to drop the moon to its current orbit would be about -40 m/s, so you’d need a million such ideal impactors to achieve your goal. Do you think there would be any lunar surface left unmelted?
“By convention, investigators treat this as a negative. It represents the energy one would need to break out of an orbit”
Any trivial input of energy will break you out of one orbit and enter you into another. The total energy of an orbit (a negative number for bound orbits) is the energy debt that must be paid to lift the satellite to an infinite distance from the primary. A total orbital energy of zero means that the satellite will coast away, reaching zero velocity at infinity. A positive orbital energy means the satellite will zip away on a hyperbolic trajectory.
“and thus:
E \alpha \left \lbrack \dfrac{M}{P} \right \rbrack ^ \frac{2}{3}
” You neglect the negative sign; bound orbits have negative energy. More mass in the primary means that the energy of the orbit is more negative; a smaller period (faster satellite, closer in) means the orbit is more negative as well.
“Thus:
E_t = \dfrac{6.673 \times 5.936 \times 7.349}{2 \times 3.844} \times 10^{24+22-11-8} = 3.786 \times 10^{28} J
”
Substitution error. M = 5.9736e24 kg. So E = -3.810 e28 J using your values. Don’t forget the negative!
“The original value was 6.383 percent higher, so the moon lost this much energy:
E_b – E_t = 3.786 \times 10^{28} J \times 6.383 \times 10^{-2} = 2.417 \times 10^{27} J”
Algebra error. This value is 6.383 percent smaller than the original value, which was -3.810e28/0.93617 = -4.07e28 J. So the moon lost -4.07e28 – (-3.8e28) = -2.598e28 J. Close enough, but the principle is important.
“That much bombardment must have transferred heat to the moon, perhaps as much as that 2.417 octillion joules, perhaps more, perhaps less.”
What sort of impacts are you proposing that would have transferred _less_ heat to the Moon than 2.598e28 J? Elastic collisions in which the impactors bounce off?
“The efficiency of any particular strike (that is, how much energy went into changing the orbit of the moon instead of wasting as heat) depends on how far the lunar material would compress under that strike.”
Unless you have some other model of impact in mind, the ‘efficiency’ of an inelastic collision depends on the ratio of the two masses involved. Momentum is conserved but kinetic energy is converted into heat. It would be good to state what collision model you are using that justifies this statement.
“Those who suggest the moon would have melted under the bombardment, might have assumed the moon got hot before it got hit. This cannot be correct. If the age of the moon is 4.5 billion years, the moon might then have been not only molten but vaporized. No: the moon got hot when it got hit, and because it got hit.”
I suggest that any bombardment that would have changed the orbital energy of the Moon by 6% within the last 6000 years would have melted the Moon, at the very least. Why would the Moon have been vaporized when it was hit if it is 4.5 billion years old but not vaporized if it was under 6000 years old?
“Each mascon lies deep to a lunar “sea.””
No.
“The maria all have basaltic floors.”
By definition, yes, maria have mare basalt. But not all mascons have mare basalt at the surface; they are not all in maria. The very paper you quoted models two known mascons: one with mare infilling (Humorum) and one without (Freundlich-Sharonov). Per the paper: “Mascon formation seems ubiquitous in lunar basins, whether mare-filled or not, despite their formation by impacts (a process of mass removal that leaves a topographic
low, which normally implies a negative gravity
anomaly…”
“Now consider: suppose one of the fragments of Cruithne’s Big Brother fell, not to the moon, but to the earth? The Laki example clearly shows a big-enough meteor could kick up enough dust to affect the weather at the sources of the Nile.”
Where? How big? Northern hemisphere, like the Iceland eruption?
“Why didn’t anyone see that bombardment? Because it likely happened during or within days of the dark of the moon.”
Why is that more likely than at any other time?
“Even such high-energy impacts, enough to produce lava flows, might not have produced flashes of light anyone could see that close to the sun. ”
A single impact of the type modeled in the Science paper would have released about 2e25 J of energy; that’s about the same amount of energy that hits the Earth from the Sun over ten years. I think a flash as bright as the Sun would have been picked up on. And nobody noticed the glowing Lunar surface afterwards, with vast expanses of white-hot lava deforming the familiar face of the Moon? They didn’t comment on the sudden transformation as the blasted face of the Moon came into sunlight over the next weeks? They didn’t make note of the fact that the Moon was now tidally locked (maybe it was before, too – you haven’t said)?
“These large impactors fell mainly on the leading face of the moon.”
Based on what evidence or calculations?
“They unbalanced the distribution of mass and thus turned that leading face toward the earth permanently in tidal lock”
Based on what evidence or calculations, other than simple assertion? Was the Moon tidally locked before, just in a different orientation, or did the impacts make it so lopsided that it became locked? How long did the locking or re-orientation take? If the Moon wasn’t tidally locked before, what was its rotation rate? If it was locked before, what was the previous orientation? Nobody commented on the fact that the Moon stopped spinning? Or that it seesawed back and forth for years or centuries before coming to a rest? Or that its face was hazy from volatiles boiling off and debris in Lunar orbit?
“Before the tidal lock happened, innumerable impactors fell on the moon, predominantly during its crescent phases.”
This implies a moon that was not tidally locked before the bombardment, but it’s unclear. Why would impactors have fallen on the Moon predominantly during its crescent phases? If the Moon was sweeping up material that was in Earth orbit, the lunar phase wouldn’t matter. If the material was asteroidal junk in Earth-crossing orbits, the lunar phase wouldn’t matter, and the Earth would have swept up more stuff than the Moon anyway.
“At least one of these companion asteroids drifted inside the Roche limit of the moon and broke up into several large fragments.”
Claimed, but not modeled or demonstrated in any way.
“These fell to the moon, started the lava flows that formed the maria, and also robbed the moon of about six percent of the orbital energy it once had.”
Absolutely no support for this claim. Are the maria all the same age? How much mass, traveling how fast, is needed to subtract 6% of the Moon’s orbital energy? What sort of collision is proposed, and what amount of heat would have been produced in the collisions? Remember that the smaller the impactors are, the more of their kinetic energy goes into heat rather than changing the momentum of the Moon. If you’re relying on the 50 km diameter impactors described in the Nature paper, you’ll need a million of them landing just right to slow the Moon down enough: not 5 as you describe. They will pump 2.41e31 J of heat into the Moon, which is the total solar output for a day, or ten times the gravitational binding energy of Mercury, or about 200 times the energy needed to blow the Moon to plasma at infinity.
“But at least one fragment fell to earth. This high-energy impact threw up enough dust to disrupt the weather at the sources of the Nile River”
Where did it fall? Did the dust disrupt weather worldwide? Do the tree rings and ocean sediments and ice cores show the effects?
“The same impacts that dropped the moon into a lower and shorter orbit, also gave the moon its heat. ”
Bald assertion.
“We do not have precise-enough projections of how much heat the moon is radiating away.”
(looks up at sky, does not see white-hot Eye of Sauron coalescing from a ring of orbital debris). No, I’m pretty sure the moon isn’t radiating enough heat to cool it down from the kind of orbital bombardment you’re talking about in the last 5300 years. I think the onus is on you to show how it could have happened, not just assert that it did happen.
I realize that I quoted some numbers related to energy release in my previous post without explicitly showing the work involved, which is something that I chide you about. I also found a powers-of-ten math error of my own; so, in the interests of full disclosure:
A collision between an impactor with radius 25 km, density of dunite (3.5 g/cc), and velocity of 15 km/s impacting vertically, would result in the following: where impactor volume is 4piR^3/3, or 6.54e13 m^3, total impactor mass is (6.54e13 m^3)(3250 kg/m^3) = 2.13e17 kg, and the mass of moon is 7.347e22 kg.
For an inelastic collision, momentum is conserved. If the frame of reference is initially at rest relative to the Moon, the starting momentum of the system is m1v1. This is equal to the total momentum after the collision: (m1 + m2)v2.
m1v1 = (m1 + m2)v2
v2 = m1v1/(m1 + m2)
v2 = (2.13e17 kg)(15000 m/s)/(2.13e17 kg + 7.347e22 kg)
v2 = 0.04 m/s – This was my mistake; I previously stated 0.00004 m/s, or 1000X less. I regret this embarrassing error.
For the inelastic collision, the initial kinetic energy of the impactor is 1/2(m1(v1)^2):
= 1/2 (2.13e17 kg)(15,000 m/s)^2
= 2.40e25 J
The fraction of kinetic energy lost in the collision is m2/(m1 + m2):
= 7.346e22 kg / (7.347e22 kg + 2.13e17 kg)
= 0.999997
Thus 99.9997% of the kinetic energy of the impactor is ‘wasted’ as heat rather than going in to slowing down the Moon. That’s effectively 2.4e25 J delivered as heat per 50 km diameter impactor event.
So, how many impacts of the type modeled in the Science paper do you propose would be necessary to change the Moon’s orbital energy by 2.417×27 J?
If we assume that it takes 1000 such impacts, striking dead vertically on the Moon’s equator, that will add ~2.4e28 J of heat to the Moon. Fortunately this is a lot more manageable than the 2.4e31 J that I estimated before using the erroneous change in the Moon’s velocity; however, it is still approximately the same as the Moon’s total kinetic energy of 3.8×28 J. Imagine the Moon traveling at its current mean orbital velocity of ~1km/s slamming into an immovable force field, or the Earth. Boom!
Perhaps your model uses larger impactors than the ones modeled by the _Science_ authors. Unfortunately, the link in your second paragraph no longer points to a relevant page at Dr. Brown’s website.