Creation Corner
Hydroplate theory debate acceptance?
Regular readers of this site know that a recent article on the 80 whale fossils of the Atacama Desert set off a firestorm of controversy. The prime mover of this controversy is a resident of Glasgow, Scotland, UK, named Fergus Mason. Your editor, as the voice of CNAV, challenged Mr. Mason to a direct debate with Walter T. Brown, developer of the hydroplate theory of the Global Flood.
Terms and conditions of the recorded telephonic debate offer
In In the Beginning: Compelling Evidence for Creation and the Flood, Brown gives detailed terms and conditions for two kinds of debate that he offers to have with critics of his hydroplate theory. The two kinds of debate are written and oral. The written debate, as Brown explained to CNAV today, is an effort to produce a book showing both sides of the issue. This massive undertaking would need at least a man-year of work from Brown and at least a man-year from any team of opponents.
If you know any credible individuals who disagree with the hydroplate theory, but will not enter a written, publishable debate as explained on pages 485–487, here is their opportunity to show orally, before a potentially large audience, that they have a scientific case.
In fact, Brown told CNAV that he would welcome a challenge from anyone willing to abide by the terms and conditions, no matter what his or her schooling, training or experience. To reply to one persistent question, Brown will hold his written debate only with a PhD as either his sole opponent or as team leader. He also expects the team to work as a team, willing to accept its leader as a true captain and not work at cross-purposes. The reason is simple: he would not want to work so hard on his half of the book, only to have the other half be less than a scholarly effort.
The telephone debate offer is a much less time-consuming debate: a sixty-minute conversation, with both sides, plus a moderator, calling in to a conference-call server. Dr. Brown asks the would-be critic of the hydroplate theory to write him at phonedebate@creationscience.com to:
- Request a recorded telephone debate, with further written exchanges as needed, and
- Say that he or she has read the relevant parts of Dr. Brown’s book.
Those parts are Part II, “The Fountains of the Great Deep,” and relevant citations and technical notes. (Those accepting the written debate offer must also be familiar with Parts I and III.) The challenger must also give the usual contact information, including name and mailing, e-mail, and other addresses, and at least one telephone number.
Procedure and rules
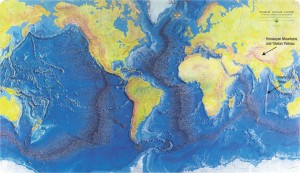
World ocean floor. Credits: Bruce C. Heezen and Marie Tharp; annotations by Walter T. Brown Jr.; used by permission
When Dr. Brown receives the letter of acceptance, he will prepare a Portable Display Format (PDF) file of his book, in its current form. (He maintains his book online, edits it ceaselessly, and was working on a key page during his interview with CNAV.) This he will “burn” to a compact disk and send it to the challenger. This will give the challenger the chance to read the most current version of the book that Dr. Brown can make available, tell him what page any particular chapter begins with, etc.
Then the two men will start negotiating where to find a moderator. The moderator must be the coach of the debate team at a leading university. Both sides must agree in selecting him, though Brown said that the third round of selection would be final. The moderator’s job is twofold:
- To enforce the rules, and
- To make sure that each side gets the same amount of time to ask questions.
This second part is important. It would forbid either side to burden the other with two many questions to answer on the spur of the moment. Some debate coaches call this argumentum verbosum (the verbose argument, proof by verbosity). Eugenie C. Scott of the National Institute for Science Education calls it the “Gish Gallop,” after Duane T. Gish, who often presents several objections to evolution in rapid-fire fashion in a debate. Dr. Brown explained to CNAV that he would not use such a technique, and that neither the format nor the moderator would allow it from either side.
The rules are simple:
The opponent must read all the material that Dr. Brown asks him to read. (He cannot challenge the hydroplate theory effectively if he does not do this.)
Neither side will appeal to religion in any way. That means that neither side will:
- Refer to the Bible or any other religious writing,
- Make fun of a deity or religious belief, or
- Use a religious writing to support a scientific claim.
Supporting a scientific claim that happens to agree or be consistent with a religious writing would not break this rule. But citing the religious writing as evidence, would.
To enforce the read-in-advance rule, the moderator must ask the challenger:
- Have you read the relevant parts of the book as Dr. Brown ask? And:
- What is the first thing you find wrong with the hydroplate theory?
[ezadsense midpost]
Then the discussion will begin. But the moderator will stop it if he decides that the challenger did not read the material.
The hydroplate theory is necessarily complex (see below). So Dr. Brown offers to read any advance material that the challenger wants to send. Furthermore, if the issues that come up in the conversation prove too complex to settle at once, the two sides can agree to meet again, a month later, for another conference call, and to exchange calculations and other writings in-between.
The hydroplate theory in summary
The hydroplate theory is Dr. Brown’s attempt to explain twenty-five different mysteries about the earth, the moon, and the solar system. They include:
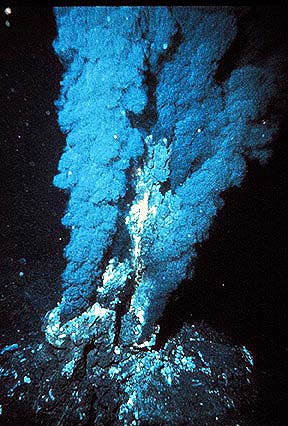
- How did the Mid-Atlantic Ridge and other ridges in the ocean form? (And what is the nature of the Black Smokers that bubble up out of the ridges to this day?)
- What produced the great heat at the earth’s core?
- What produced the trenches that surround the Pacific Ocean, and the Ring of Fire?
- What froze the great woolly mammoths? (And why does one find tropical-like vegetation in the Arctic mammoth graveyards?)
- How did the Grand Canyon form?
- Why do the continents fit together like a gigantic jigsaw puzzle?
- Where do comets, asteroids, and meteoroids come from? (And why do comets have twice the proportion of deuterium in the earth’s oceans?)
- What really formed the radioactive elements that are present on land, but never on the ocean floor?
The answers to those questions are often shocking and surprising at first reading (as your editor can directly attest). But the hydroplate theory is entirely self-consistent. Dr. Brown has refined his theory for more than thirty years.
The current challenge
Your editor challenged Mr. Mason last week, after Mr. Mason said that he had two bachelor-of-science degrees, one each in biology and astronomy, and suggested that his schooling and training were better than those of Brown in the subjects at hand. He suggested that CNAV forward his e-mail address to Brown. CNAV did, and Dr. Brown replied directly to Mr. Mason and reaffirmed his challenge.
Dr. Brown still needs Mr. Mason to reply formally to his last message, in the form that Dr. Brown has set forth (see above). He suggested that Mr. Mason should not consider his challenge accepted until he actually makes it in that form. He also suggested that he and Mason could copy CNAV on all their correspondence, an arrangement with which CNAV would agree.
CNAV also is ready to publish the transcript of the debate as soon as Dr. and Mrs. Brown prepare one, and Mr. Mason approves it as to form and content.
Related:
[amazon_carousel widget_type=”ASINList” width=”500″ height=”250″ title=”” market_place=”US” shuffle_products=”True” show_border=”False” asin=”1878026097, 0890515077, 0310234697, 0875523382, 0890511586, B002RBHDFK, 0949906689, 0890513600, 089051416X, 0890515050″ /]
[ezadsense leadout]
Terry A. Hurlbut has been a student of politics, philosophy, and science for more than 35 years. He is a graduate of Yale College and has served as a physician-level laboratory administrator in a 250-bed community hospital. He also is a serious student of the Bible, is conversant in its two primary original languages, and has followed the creation-science movement closely since 1993.
-
![CHAPTER 10: Objective Reality Is Required for a Free Society Space Is No Longer the Final Frontier—Reality Is [upcoming release May 2024]](https://cnav.news/wp-content/uploads/2024/04/Objective-reality-v-acceptance-400x240.png)
![CHAPTER 10: Objective Reality Is Required for a Free Society Space Is No Longer the Final Frontier—Reality Is [upcoming release May 2024]](https://cnav.news/wp-content/uploads/2024/04/Objective-reality-v-acceptance-80x80.png) Education5 days ago
Education5 days agoCHAPTER 10: Objective Reality Is Required for a Free Society Space Is No Longer the Final Frontier—Reality Is [upcoming release May 2024]
-

 Human Interest4 days ago
Human Interest4 days agoIdaho prepares to defend its abortion ban
-

 Education2 days ago
Education2 days ago‘Grading for Equity’: Promoting Students by Banning Grades of Zero and Leaving No Class Cut-Ups Behind
-

 Civilization4 days ago
Civilization4 days agoEarth Day Should Celebrate U.S. Progress & Innovation
-

 Civilization3 days ago
Civilization3 days agoNewsom plays silly abortion politics
-

 Family1 day ago
Family1 day agoIdaho defends against abortion mandate
-

 Education4 days ago
Education4 days agoThe Intifada Comes to America. Now What?
-

 Civilization4 days ago
Civilization4 days agoEarth Day – part of cultural Marxism
















There’s a better way. Brown can take his (cough, cough) “theory” to a geological conference, and get laughed out.
He who laughs last, laughs best.
He who laughs last didn’t get the joke in the first place.
The joke’s on you, and on the hoity-toities that run professional conferences these days, and organize conferences on things like “Dark Energy.”
IOW Brown has too much pride to wash the feet of the scientific community? His behavior seems distinctively anti-Christian as a result.
Your argument assumes that what you call “the scientific community” are acting in good faith. They aren’t. On the other hand, Brown puts his theories out for anyone to see. They include some very detailed technical notes that form part of the “homework” that any debate challenger needs to do.
Your argument assumes that Brown is acting in good faith. He has presented no evidence to support that assumption. His hoity-toity attitude, where only HE deserves special dispensation by HIS rules, constitutes evidence that Brown does not act in good faith.
Well now, why don’t you read his book and then tell me what’s wrong with it? He also explains where those rules come from, by the way.
It’s far easier to state what’s actually correct about the book: the intellectual equivalent of spelling the indefinite correctly. Seriously, correcting the errors would require an encyclopedic effort covering tens of thousands of pages; it’s THAT wrong.
Terry wrote:
Brown puts his theories out for anyone to see. They include some very detailed technical notes that form part of the “homework” that any debate challenger needs to do.
Geno answers:
I would love to see Brown’s “very detailed” calculations regarding the disposition of the heat energy from all that 700F water and the latent heat of condensation as all that steam returns to liquid form.
As I recall, I came up with a mixture of steam and water around 55-45 at the boiling temperature of water…. then, that steam still has to condense, of course. In doing so, it MUST release the latent heat of condensation.
At least get your facts straight Hurlbutt, PDF is a Portable Document Format.
Quibbles. That doesn’t change the Ts and Cs that Brown sets out.
See, the issue here is that Mr. Brown came to a conclusion, then finds “evidence” to support his views. That is not science. That is literally the exact opposite of science. There is no way to actually have a scientific debate if the premise of the “theory” is inherently flawed from the very start.
First, if you actually read the book, you’d be hard-pressed to make that kind of case.
Second, you have described what evolutionists do. So all you’re doing is throwing off on him. You didn’t really think I’d let you get away with that, did you?
I did indeed read the book, and I’m astonished that someone with even a cursory biology education would completely ignore 5 of the 6 kingdoms of life when describing the possibility of a global flood. That strike me as someone who was clearly looking for evidence to support his conclusion, not someone making an unbiased conclusion after making observations and recording evidence.
I don’t see what the problem is. You know that only one kingdom, the animal kingdom, needed the kind of salvage that Noah performed. In any event, your complaint is incomplete at best.
No, I know that plants, most fungi, coral reefs, billions of bacteria, archaea, and protists can’t survive in deep salt water. There is no explanation that allows plants to have survived the flood without massive amounts of macroevolution happening in a few thousand years. The earth couldn’t exist in it’s current state if It had been previously covered with salt water. Additionally, the lack of plants would have caused all the herbivores to starve. There is no scientific reconciliation of these facts, it must be a work of divine intervention, or the flood didn’t happen.
If you had read the book more carefully, you would have noticed that the salt concentration was not the “deep salt water” that we see in the oceans today, but was far more dilute.
If the salt water of today did not exist a few thousand years ago, then you’re implying that the majority of “fishes,” for example, EVOLVED adaptations to live in today’s salt water. Obviously you accept evolutionary changes on a relatively large scale, and this is merely one example of such acceptance on your part.
They had to adapt to it, certainly. Adaptation to environment is not the same as one species giving rise to another.
Brown estimates that the earth’s oceans, and the water they contain, doubled in volume and quantity during the Flood. The concentration has occurred since then, In fact, at current rates of salt deposition in the oceans, the ocean would have turned to inhospitable brine within a few thousand years, not the billions you postulate.
And one more thing, smart boy, since you said you read the book. Here’s a direct quote, that Dr. Brown was kind enough (man, was he up late!) to point out to me in the early-morning hours:
“I’m astonished that someone with even a cursory biology education…”
Check out Dr Brown’s biology qualifications. It won’t take long.
Johnny: Mr. Brown came to a conclusion, then finds “evidence” to support his views …
Hurlbut: you have described what evolutionists do.
Rubble: If that’s truly the case, please cite a specific example from the professional science literature to support your claim. Your pending failure will reveal the falsehood of your claim.
Start with Ernst Haeckel and his comparative-embryo drawings.
Continue with Java and Nebraska “men” that turned out not to be “men” at all. (Piltdown Man was a special case: some hucksters took an ape specimen and deliberately tried to pass it off as an ancient man when they knew it wasn’t.)
And the literature? I could cite the entire body of literature. But I’ll limit it to the part I know about best of all: the radiometric dating paradigm.
Why did Geochron Laboratories date five samples as being of five different ages, when they all came from a lava dome laid down ten years earlier?
Why did different laboratories come up with two different ages for samples of basalt, and yet another age for a tree buried in it?
Are you willing to admit that radiometric dates are often non-correlating and inconsistent? The Grand Canyon presented a prize example about six years ago.
And don’t hand me “peer review.” Climategate proved what a sham “peer review” can be.
You can’t be serious. Would you have us believe that Evolution is not based on the presumption that EVERYTHING had to evolve through natural causes?
Pure scientific “assumptions” are as unrealistic as social utopia. Like it or not, we all have a worldview. The question realistically is which worldview is best supported by the science?
Furthermore, it astounds me that whether you are a Creationist or an Evolutionist, most do not consider that ALL theories are subject to refinement. One glitch in the presupposition, and all are ready to throw the entire theory out. Please remember that the discussion is about theory and not scientific law.
RoseAnn, we need to clean up some misunderstanding.
First, you seem to think that a “proven” scientific theory “grows up,” as it were, to become a scientific law. That is incorrect. If anything, laws “grow up” to become full-blown scientific theories, where the “law” is generalized over a broader set of cases.
Second, scientific laws hold only under specific circumstances. In your words, “one glitch in the presupposition” and the so-called “law” goes out the window. A good example is Newton’s second law of motion, F=mA, where F and A are vectors. This law breaks down when m (mass) is very small, or when the velocity scalar component approaches c (speed of light), just to give two familar circumstances under which this law breaks down.
Third, and perhaps most radically in your view, evolutionary theory does not require “that EVERYTHING had to evolve through natural causes.” There are at least two problems with claiming otherwise.
In principle and in practice, we cannot scientifically investigate supernatural causes. That does not mean that there are no supernatural causes; it simply means that science is the wrong toolkit for determining whether there are supernatural causes or not. This is often paraphrased as “you cannot put God into a test tube.”
The other problem is that we can often determine if humans have intervened in an evolutionary process. Arguably, such intervention is “artificial” and thus not “natural.”
Science can, however, determine that some things must have had a supernatural cause. What we hear so often from evolutionists and uniformitarians is a deliberate attempt to say that nature, and matter, are all there are.
Terry wrote:
“Science can, however, determine that some things must have had a supernatural cause. ”
Geno answers:
Really? How? What test for a supernatural act is available to science?
The problem is that science relies on the constancy of natural laws. Supernatural acts, by their very nature require a suspension of those laws. Because of that, they fall outside the scope of scientific inquiry.
The test for a supernatural cause is simple: anything that shows that something undoubtedly happened, and that natural laws make that something impossible, then something, or some-One, overrode nature to make it happen.
That definitely applies to creation. Logically it applies to prophecy, or the accurate prediction of a future event, especially when the odds against said event occurring exactly as predicted are longer than nineteen to one. (That is the conventional threshold test for significance: when the probability of an event is less than 5 percent, one rejects the null, or non-intervention, hypothesis.)
Terry wrote:
The test for a supernatural cause is simple: anything that shows that something undoubtedly happened, and that natural laws make that something impossible, then something, or some-One, overrode nature to make it happen.
Geno points out:
As our understanding of the workings of nature is still developing, I see your comment as little more than a “God-of-the-gaps” position. We both know the history of that one.
Then I commend to you the task of establishing the sequence of events, the total probability of which was greater than fifty percent, that produced the first cell that became the common ancestor of all other living things. Not to mention a universe, and a planet, hospitable for the same.
[…] Hydroplate theory debate acceptance? […]
Oh, I see. Somehow, the plants and fungi and bacteria and protists and archaea magically managed to survive months of total submersion in less salty water, without light or usable oxygen. The fact that the ocean was less salty was my strongest point, and obviously by addressing that fact and that fact alone, you have proven that plants can survive under crushing amounts of water without light or usable oxygen. Additionally, the salt water left behind totally wouldn’t have been concentrated and literally salted the earth as it receded.
Terry, you don’t use a debate to show that a theory is correct. It’s tested through the collection of data, matching results to hypotheses, repeated testing, control groups, peer review.
If Col Brown has enough evidence to support his claims, other than “because I said so” let him present it to his peers – fellow geologists. Yes, he might be laughed off stage – he wouldn’t be the first to be laughed at and then proven right.
But at least it’s better than hiding behind vague conspiracy theories and offers to debate unknown people on the internet. Who is Fergus Mason anyway? Why not debate an MIT geologist – that would be more constructive. And as it’s a debate, you wouldn’t have to worry about censorship, etc. This is a theory that could rock the world of geology as we know it. Debating unknowns on the internet isn’t going to publicise it.
Just a random ex-soldier with an interest in science and a deep dislike of unqualified charlatans like Brown.
Enough to take him on, as you said you would? You did say that you looked forward to debating him. He’s still waiting to hear from you, per the instructions in this article.
I would also like to see Mr. Brown present his research at ANY scientific conference. I am actually at the AGU fall meeting in San Francisco this very moment, along with 20,000 other scientists who are all presenting evidence that conflicts directly with everything Brown proposes. Anytime someone finds a problem with another’s research here (or at any meeting), they publicly ask them about their methods and the educated community present can make an informed decision on the subject. Sure, Brown wrote a book. But thousands of scientists have written hundreds of thousands (millions maybe?) of publications, and then proceed to defend those works to critiques. Brown has not. If his “theory” can hold up to scientific inquiry, he should present it to other scientists rather than this vain attempt to stir up criticism of mainstream science and perpetuate conspiracy theories in internet chat boards. And don’t give me some “the establishment wouldn’t let Brown present” nonsense. We both know that he hasn’t made an effort to get his work into mainstream science, and the reason for this is likely because he knows it will be torn to shreds by people who actually understand the science. The reason real scientists with phds haven’t debated him is because they either: don’t know who he is, don’t know anything about his theory, don’t see how any one can call themselves a scientists while basing a theory off of a 2500+ year old book, or all of the above.
Pardon any spelling/formatting errors. Like I said I’m at AGU and have been writing this out on my phone.
Well, now. If you’re so sure that you can take him on, why wait for Fergus Mason to complete his follow-up? Why don’t you request a debate with him?
Because frankly I don’t care what Mr. Brown has to say about the subject. He has no evidence, and I would rather spend my time doing something constructive. and it doesn’t really matter what the outcome of the debate would be. His theory would still be considered a joke by any geologist/ecologist/physicist/biologist/scientist. Besides, Brown doesn’t meet my qualifications for a debate. He demonstrates a clear lack of understanding of basic geologic and biological processes. I don’t care if he has taken a few basic geology classes, that is not adequate to understanding the subject.
And well now. Brown is so sure of himself, why can’t he present his data to other scientists like everyone else? why must he promote it only to laymen (I don’t mean for this to be derogatory, just being honest) who don’t understand the subject? Let’s see him submit his work to scientific community to be properly critiqued? Or is he afraid of the result?
If your attitude is at all typical of the professional conference that I believe you said you are attending, they wouldn’t let him in the front door. Why? Because he didn’t play the credentials game. Nevertheless, he has far better understanding than you seem willing to give him credit for.
A joke, eh? Well, the joke will be on his detractors, eventually. History is replete with stories like this. Phlogiston, caloric,…the list has no end.
Mr. Hurlburt, once again you have no idea what you are talking about. I don’t blame you, your background is in medicine so presumably you’ve never attended a physical science conference. Actually, anybody is allowed in the front door so long as they pay the registration fee. The public are more than welcome, and pay considerably less to attend (less than have the cost) than researchers or people presenting their work. This is the case with every geoscience conference I have ever attended (including AGU, DPS, LPSC, and GSA). Mr. Brown (or you, for that matter) would be free to critique all the “pseudoscience” you wanted to. If Brown wished to present, I’m sure he could, provided he was actually doing something scientific (as opposed to religious). In other words, if he had evidence for a global flood, I am positive that it would be a very popular presentation. AGU is the worlds largest science conference, with tens of thousands of presentations on current research in the natural sciences, and as such would be an ideal location for Mr. Brown to present his work.
Furthermore, a key concept of science is that no theory is ever perfect, and ideas are made better by input from others who are educated in the field. Mr. Brown could gain new insights by seeing the work of other earth scientists.
So I must ask again, had Dr. Brown EVER submitted an abstract to present his theory at. Scientific conference? And if not, why not? Is there a reason why he won’t share his work in the way that every single other scientific professional (including those in engineering and medicine) do?
The reason is that any editor of any journal will accept for publication only a manuscript that no one else has ever published. In short, they always insist on first rights. Which they can’t get. First rights expire with the first publication.
Now it’s all very well for you to say that Dr. Brown’s evidence would be “a popular presentation” at the venue you are, I presume, submitting this from. You will forgive Dr. Brown and myself for being skeptical. Once again, your attitude gives you the lie.
The “first rights” excuse is just that, an excuse. Allegedly the hydroplate theory generates predictions that can be investigated through new scientific research, beyond the (cough cough) “original scientific research” embodied in his previously published text. If this were truly about science, Brown can easily conduct and/or supervise such new research, generating new publishable material.
But Brown doesn’t do this. A good scientific theory is the driving engine of successful scientific research, not merely the result. Brown has to defend his work on new scientific research driven by his ideas. Otherwise, he’s hardly more than a drunken Monday morning quarterback, slurring out claims that he can play better than the pros.
That’s a matter of opinion. I judge otherwise.
A matter of opinion? IOW you’re defending the sloth of Brown? You think that a good scientific theory does NOT drive successful scientific research?
I defend Brown’s position, but I reject out-of-hand your evaluation of Brown or his work.
Now if you think that you can show him up, why not follow the e-mail link and offer to debate him over the telephone?
You claim that “Brown offers to read any advance material that the challenger wants to send.” I challenge the veracity of that claim, and for a simple reason: I see no evidence that Brown has seriously read the professional scientific literature on these matters. Rather, I see the classic dishonesty of the professional Creationist: cherry-picking and quoting out-of-context. I don’t see any honest effort by Brown to seek out the passive challenges to his ideas.
So in essence, you’re asking me to debate a dishonest man. Sorry, but he must first demonstrate his honesty to me. That is one of MY conditions to debate.
Prove that that’s not a cop-out. Make your request, and express your concerns to him.
Prove that he’s honest about these matters. Until then, you’re telling me that it’s OK for Brown to impose conditions, but his opponents cannot do so.
Why won’t you ask him?
I have no reason to expect honest answers from Brown. That is why I do not bother to ask.
Let’s tally the score.
Brown insists on forcing conditions upon others that he will not tolerate in kind from his opponents.
Brown’s work is scarcely more than an unsupported claim that modern science be should abolished, because his own work is allegedly superior.
I probably missed a few things.
I think you did. So I repeat: why not ask him?
What I don’t understand is that if the world’s oceans were made so dilute during this enormous flood, then where did all the great salt strata come from? Salt is only deposited when brine is supersaturated, yet we find salt deposits between different strata which were supposedly laid down during the Noachical flood.
OK. Remember that the Flood waters came from underneath the crust. They came, to be specific, from a subcrustal ocean that was three-quarters-of-a-mile deep, and lay ten miles below ground. That water was heated and compressed to supercritical temperature and pressure.
Supercritical water is a powerful solvent. Basically it started to work its way into the crust above it, and the mantle below it. (In fact, a black basement-layer-like formation called the Moho forms the boundary where the erosion reached.) So that water dissolved a lot of minerals. All those minerals came up during the breakout and shortly thereafter.
But the salt had precipitated out long before, and lay at the bottom. Now this salt came up and ended up trying to force its way past several layers of heavy sediment that formed when the water chewed up the separated ends of the crust for 800 miles in each direction. Salt, being lightweight, formed domes. See here, and search for the phrase “salt domes.”
Terry wrote:
Remember that the Flood waters came from underneath the crust. They came, to be specific, from a subcrustal ocean that was three-quarters-of-a-mile deep, and lay ten miles below ground. That water was heated and compressed to supercritical temperature and pressure.
Geno points out:
It is worth note the critical temperature for water is over 700F (about 375C). Brown has half of the modern oceans coming from this undergound chamber at a temperature very near that. Just consider what would happen as all that steam is absorbed into the atmosphere then condenses (releasing a HUGE amount of heat energy) before it can fall to the surface.
Hint: The condensation of enough water vapor to cover the planet to a depth of only one meter (less than 40 inches) releases enough enough energy to heat the atmosphere by 240C (432F). We cook Thanksgiving dinner at cooler temperatures.
That’s a pretty slick answer as there are indeed deep layers of salt which form diapirs in deep sediments but fails to address the enormous layer of salt that runs across northern Europe which is part of an evaporation sequence of dolomits, gypsum and anhydrite, and halite that differentialy precipitate with water evaporation and has obviously been laid down in situ. How do we know that? Well the salt is a cap rock for the natural gas fields of the southern North Sea and has been extensively mapped by oil companies using seismology and drill cores, so it is something we know a lot about. It is itself the source of some salt domes but there is no evidence that it originates from one of your salt domes. Things get more complicated for your ‘theory’ (in scientific terminology it barely qualifies as an hypothesis) when you consider the fact that these evaporate deposits don’t just correspond to a single event but actually shows three major evaporational cycles
Here’s the interesting part: if you’re going to talk about evaporation sequences, then you have to admit that northern Europe, among other places, was under water. Really, I don’t see what your problem is with Dr. Brown’s theory, other than the time frame.
Given that every secular geologist freely admits that most rocks have been deposited in a marine environment I fail to see how your smug reply proves anything; it certainly doesn’t necessitate a global flood. I find it hard to belive that you really don’t understand anything about the secular geology which you are contesting. You fail to deal with the fact that were multiple evaporation sequences which are sandwiched between other sedimentary rocks which are not uniformly sorted as a creationist flood would imply. There are multiple reasons why Mr. Brown’s theory doesn’ stand up to scientific scrutiny without some supernatural intervention.
And I reply that your “multiple reasons” and “multiple evaporation sequences” are “multiple guesses.” Which, need I remind you, are no-noes in the scientific method. William of Occam said that one must not multiply guesses without sufficient reason. And the only reason that the secular scientific community has ever given for their multiplicity of guesses is that they just flat-out refuse to accept that a certain ship’s log, that is part of a supernatural narrative, has any probative value whatsoever.
If the story of Noah’s Flood actually held up to scrutiny by observing physical data, then sure: we could agree that Genesis has probative value. The problem is twofold: there are no physical data that require such Flood, and there are physical data that directly contradict it.
You’ve been presented with a classic set of such contradictory data: salt beds that are stacked atop of one another, separated by non-salt bed deposits. I remind you that such deposits, for both the salt layers and the interbedded non-salt layers, typically have fossil deposits. Brown offers no explanation that reasonably explains this set of data.
But then, none of this matters to you. Physical reality is low on your set of priorities. Without hesitation, you would erase the last century of science at a minimum, and probably erase the majority of the century’s science previous to the last century as well. The proof of such rejection is your flippant willingness to discount the entirety of the professional science literature and conferences.
On the contrary, Brown has no problem with any of the data you cite.
And as for dismissing the last century and a half of origins science without hesitation, I remind you: Charles Lyell, Charles Darwin, and Henry Wallace equally “casually” dismissed millennia of understanding of the origin of life and the origin of the earth. Don’t tell me that any theory gains authority from time alone. Not when you are not willing to give the same consideration to a theory that you oppose.
Of course the “ship’s log” which you tout as evidence is nothing of the sort. For a start it wasn’t written by Noah otherwise it would have been a first person narrative; there is no physical log to be analysed by archaelogists. The best that you can say is that it is a sailor’s tale which was passed on and embellished in a series of Chinese whispers to end up no more believable than The Odyssey, Le Morte d’Arthur or The Adventures of Baron Munchausen. Mr. Brown’s PIDOOMA hypothesis doesn’t come close to explaining the majority of the world’s stratigraphy.
Want to take that up with him directly? The article contains the instructions.
Terry wrote:
Really, I don’t see what your problem is with Dr. Brown’s theory, other than the time frame.
Geno answers:
WOW ! ! ! !
How about the heat issues? Tell us, Terry, you reject much of what the evolution side says out-of-hand. Do you perform ANY “due diligence” on what creationists propose or do you simply accept it without question?
I suspect the former as you have been asked for MONTHS now to perform a few simple back of the envelope calculations that should be well within your engineering expertise. Yet, I can find no evidence you have questioned Dr. Brown’s claims in any serious manner.
######
Terry wrote:
And as for dismissing the last century and a half of origins science without hesitation
Geno points out:
The flood takes place well after origins. As such, it’s a real stretch to call it “origins science” in any way at all.
######
Terry wrote:
the only reason that the secular scientific community has ever given for their multiplicity of guesses is that they just flat-out refuse to accept that a certain ship’s log, that is part of a supernatural narrative, has any probative value whatsoever.
Geno points out:
First, as a sailor with over 12 years naval experience, the Genesis flood account does not qualify as a “ships log.” Further, since Dr. Brown says he does not rely on the supernatural, “a supernatural narrative” has no value in a discussion of his model. Finally, revelation is only an “eyewitness account” to the one who receives it…. to all others it’s hearsay.
I had said, to Terry:
Do you perform ANY “due diligence” on what creationists propose or do you simply accept it without question?
I suspect the former …..
That should have been “I suspect the latter….
Do you perform any due diligence on what uniformitarians and evolutionists propose, or do you simply accept it without question? I suspect the latter.
And: what’s this? A sailor with twelve years’ experience? I should advise you: I’m getting an awful lot of boasts in this comment space, and I begin to suspect deliberate credential inflation. Tell me: where was that twelve years? In the Navy? The Merchant Marine? The fishing fleet? Or where?
Terry challenges:
And: what’s this? A sailor with twelve years’ experience? I should advise you: I’m getting an awful lot of boasts in this comment space, and I begin to suspect deliberate credential inflation. Tell me: where was that twelve years? In the Navy? The Merchant Marine? The fishing fleet? Or where?
Geno answers:
United States Navy, November 13, 1967 thru May 12, 1980. Rank at discharge ET1 (SS). Conducted five Polaris deterrant patrols on the USS James Monroe (SSBN 622). Spent four years on the USNS Range Sentinel (TAGM-22) which served as a floating “blockhouse” for the at-sea launch of Posiedon missiles and the sea tests of the Trident Missile.
You have my email address…. if you want a copy of my DD-214, let me know.
I’ve paid my dues for our freedoms. So has Dr. Brown. …. how about you.
Terry wrote:
Do you perform any due diligence on what uniformitarians and evolutionists propose, or do you simply accept it without question? I suspect the latter.
Geno answers:
Non-responsive “answer” noted.
Those things that are within my expertise, I check. Dr. Brown’s clais are well within the expertise of an engineer to check out. Why won’t you do it?
You may have satisfied yourself that I haven’t done due diligence on Walt Brown’s theory. Well, copy this, sailor: I have checked his calculations, and even discussed their basis with him, at some length. You are missing something—something egg-on-your-face big— in a place that’s easy to find.
Terry wrote:
You may have satisfied yourself that I haven’t done due diligence on Walt Brown’s theory. Well, copy this, sailor: I have checked his calculations, and even discussed their basis with him, at some length.
Geno answers:
I’ve seen no evidence of it. You’d think after months of asking, you’d show just one example.
#####
Terry wrote:
You are missing something—something egg-on-your-face big— in a place that’s easy to find.
Geno answers:
Yeah? What?
Please do come up with that “refrigeration effect” argument again. I’ll be happy to discuss with you how much “refrigeration” we’re going to get from 700F steam. There’s a reason we don’t use boiling water to cool our homes.
How about my use of the Steffan-Boltzman equation to calculate the radiation of energy to space? You are correct, Steffan-Boltzman discusses a black body and Earth is not one. However, a black body is the IDEAL heat radiator …. Earth would be LESS efficient at radiating energy.
Oh yeah…. keep in mind, the instant the temperature or pressure of that supercritical water drops below (about) 700F or (about) 3200 psi, it’s no longer supercritical.
I completely agree with you when it comes to journal publications. Conferences are another story. Even if Dr. Brown wasn’t officially presenting anything he could still come and speak with other researchers, even if he thinks that they are all completely wrong on the subject of Earth’s history. And if he had actual evidence for a global flood, that would be a popular presentation. I recall a talk a couple of years ago that also was about a global flood (the flooding of glacial lake Agassiz in Canada, which would have raised global water levels several meters. The researchers were tying it in with the flood stories that come from numerous cultures across the globe). The presentation room was packed (with several hundred people).
Something to think about: you should keep in mind a large number of the scientists here are from private companies (Big Oil is a chief sponsor of AGU), and they use what you consider “pseudoscience” to find oil, mine minerals, etc. I’ve mentioned this before on this website but it can’t hurt to emphasize it again.
Once again, has Dr. Brown ever even tried to submit an abstract for a conference? And if not, why not? It doesn’t cost anything other than the time to write an abstract. And there are dozens of conferences every year hosted by a number of institutions. I’m sure one of them would be bound to accept him as a presenter.
I must be missing something with Dr. Browns idea: where did the sub-crustal ocean come from? The prevailing scientific theories give us a consistent series of events from the origins of the Earth (universe, really) to present day. Yes there are some holes, but all that means is that there is more work that needs to be done by scientists in the future. Dr. Browns theory, at least to my understanding, doesn’t explain anything prior to the flood (presumably it was all put there by God during Genesis, but that is not really a satisfactory scientific answer, namely because it just raises the question of where God came from. But that’s an entirely different topic for an entirely different argument).
So does Dr. Brown have an answer for how the “fountains of the deep” got to be underground in the first place? His call for a debate says that nothing religious or supernatural can be the topic of discussion, so I am understandably very interested in his explanation.
Dr. Brown seeks to explain the Flood itself. And whether or not he can say why the earth formed with a sub-crustal ocean (and in fact, he says that the earth did not so much *form* as *was created*), he can definitely show that a subcrustal ocean once existed. And remnants of it still exist. They are bubbling up out of the Mid-Atlantic Ridge right now, as the “black smokers” that have been known to oceanography since 1970 or so.
Brown is now insisting that, among other things, I tell him my employer’s name as a condition of the debate. Why does he need this? He also seems to be insisting that it be possible for the debate audience to “locate” me afterwards. As the audience is likely to include a large number of wingnuts, and I work as a military consultant, this is not going to happen. I’m negotiating with Brown to come up with mutually acceptable terms for the debate. Frankly I don’t see why he needs my postal address for an audio debate, and while I may consent to let him have it there’s no way I’m agreeing to him telling even one other person what it is.
I am privy to this correspondence. It’s like this, mate: on-line personae are ridiculously easy to fabricate and confabulate. Ask anyone who has tried to chat up someone on-line who is supposed to be a lovely girl, but who turns out to be (a) a bloke passing as a girl, and (b) a con artist from Nigeria seeking to scam him and empty his bank account. Brown seeks to learn, at least to his own satisfaction and that of the moderator, that he is dealing with a real person, and one who is exactly who and what he says he is. All this is part of, to quote another commenter on this thread, “due diligence.”
I am willing to take reasonable steps to prove my identity. I am NOT willing to give him any details of my work or to allow myself to be located by anyone else. For him to demand that I make myself locatable by the debate audience is completely unreasonable.
By the way, when you say you’re privy to the correspondence, did Brown forward you my email to him?
Yes, he did.
Fergus asked:
By the way, when you say you’re privy to the correspondence, did Brown forward you my email to him?
Geno notes:
In the early discussions between Terry and I concerning Brown’s claims, Brown did the same thing with regard to my communications. Once it became apparent to me this had been done, I forwarded my messages to Terry. If nothing else, this assured me Terry had a complete record of our exchanges.
One thing I resent to this day is that Terry did a complete article about my communications with Brown in which Terry made claims that were clearly at odds with the facts that had been provided to him. Specifically, Terry claimed I had not advised Brown of my issues with the Hydroplate model. I was able to provide clear statements by me in my initial contact with Brown specifying my objection to Brown’s model was based on the energy released. IIRC, no fewer than 6 references were made to this problem.
To this day, Terry has not even acknowledged, let alone corrected, this factual error.
I defer to Dr. Brown in my judgment of that correspondence. Not to you.
Terry wrote:
“I defer to Dr. Brown in my judgment of that correspondence. Not to you.”
Geno answers:
Yet you wonder why I have doubts about your “due-diligence” with regard to Brown’s claims. How about this… rather than “defer” to either of us, you examine the record that both of us have provided you.
Tell ya what… let’s let the readers decide for themselves whether or not I told Dr. Brown what I think is wrong with his Hydroplate Model.
Here is what Terry said with regard to my communication with Brown:
“as Brown reiterated to this Examiner, Brown was asking Castagnoli to tell Brown anything he thought was wrong with the Hydroplate Theory”
Link: link to examiner.com
Here are the facts, as documented to Terry by both Dr. Brown and myself. First, I must apologize… in my initial communication to Brown, I only mentioned my issue once:
“If you recall, my disagreement with your theory is the energy released will result in the destruction of all life on Earth. It should be fairly obvious that if the planet is sterilized, nothing else about the Hydroplate Theory matters very much.”
However, in another message which was still before you were aware I had been in contact with Dr. Brown, I said:
“you do make certain assertions of fact that (I believe) will destroy all life on the planet….
my debate question is much more focused and, as I see it, a necessary requirement to the validity of your model. That question is: “Will the energy released by the Hydroplate Model destroy all life on Earth.” If it does, nothing else in your model matters, as we wouldn’t be here to discuss it……
We can begin with whether or not your model is survivable…..
I think sterilization of the planet is a pretty significant objection that doesn’t necessarily require looking much further……
the reentry heat of 10% of the mass of the comets and asteroids wasn’t merely enough to destroy all life; it was enough to boil the entire hydrosphere….
when I first looked into your theory, you were claiming an energy release of something like ten billion hydrogen bombs. Now that has changed to “1500 trillion.” (Geno notes: the number has now increased to 1800 trillion hydrogen bombs.)…..
There is also a serious problem with adding about half the water in our modern oceans from a subterranean chamber where it was stored at temperatures of around 400C…..
When I look at the energy release you claim, it’s enough to raise every drop of water on the planet from freezing and boil it some 3000 times over. You could be 99.97% efficient at getting rid of the heat and the remaining 0.03% will still be more than enough to boil every drop of water on the planet. Looking at it another way, there is enough energy that you can eliminate 99.99995% of it any way you choose and the remaining 0.00005% will still raise the temperature of the atmosphere by a lethal 100C. I’m not aware of any natural process that has a “leakage” less than 0.03%, let alone 0.00005%……
Presumably you were in possession of these communications before you wrote your article. I do not know how I could have been more specific and explicit with regard to the issues I have with the Hydroplate Model.
Geno said:
“Brown did the same thing with regard to my communications.”
What bothers me is that Brown forwarded an email containing some of my personal data. I’ve contacted him again in an attempt to establish an acceptable basis for the debate, but I’ve made it clear that he does not have my permission to transmit any more of my personal information to anyone associated with Conservapedia and that he’s not getting any details of my work, which are irrelevant to the debate in any case.
The conditions Brown has publicised for a telephone debate only say I have to state my current job, which I did. However he’s now insisting on the name of my employer and, if I claim to work in a sensitive field, a way to verify this. I suspect he’s going to try to use my refusal to provide this as a way to get out of the debate.
Fergus wrote:
“The conditions Brown has publicised for a telephone debate only say I have to state my current job, which I did. However he’s now insisting on the name of my employer ”
Geno answers:
Well, Dr. Brown is pretty inflexible with regard to his terms for a debate. I see no valid reason you can’t be equally inflexible when he adds conditions that are not stated. j……. But that’s just me.
I intend to be. He asked me my current job, I told him and that’s all he’s getting. If he then withdraws his debate offer on the grounds that I won’t provide further details that his conditions don’t specify, well, I think people can draw their own conclusions from that.
OK, I told Brown that if he’s going to forward my emails to Terry he can do so on condition that he first removes any information I’ve highlighted in yellow; that would be information such as my home address.
He won’t accept this. The furthest he’ll go is to say he’ll “seriously consider” removing anything that could endanger my life, family, country etc. Not satisfactory.
[…] the debate might want to contact him to make sure they understood anything he said. He had by then said that he was Just a random ex-soldier with an interest in science and a deep dislike of unqualified […]
Did this debate ever actually take place?
No. Dr. Brown is still looking for someone to take him up on it (and mean what he says).
Dr. Brown’s theory is amazing. I’ve been a Christian for 27 years, and have only just now heard about hydroplate theory. I can relate to people who scoff about the Bible and believe its not “scientific,” but after God changed my heart towards Him and His Son, Jesus, my attitude on many things has been different.
In fact, my heart had been so changed by the time I first read Genesis, I remember very clearly making a decision based on faith, rather than “reason.” I embraced the Genesis account *because* it was written in the Bible, so I freely admit that my conversion came about as the result of a heart change, rather than a “reason” change.
And then I began reading accounts of Evolutionism and its theory, and how it too is a faith based assumption, (seeing as how no one was around at the time to give an account.) People believing it do so on faith, rather than on facts, (as they so demandingly insist.)
I appreciate very much your efforts to defend God’s Creation and how it came into being, and your willingness to stand against those who by force of their own arrogance, nullify and dismiss a notion contrary to their own conceits.
I appreciate Dr. Brown’s work in this book, “In The Beginning,” as I have ordered it and am working through it. I must say, it is the most engaging and complete work on creation science I have ever encountered, and am truly amazed at all the effort and consideration he has put into it. I started reading it online, but purchased the book to have as a reference. The difference between the two is almost night and day, and I can’t get over how helpful and illuminating it truly is. I’ve encountered more useful information about plate tectonics, the vapor canopy theory, the hydroplate theory, and the rational and scientific considerations that go along with them than I ever would have expected. It is truly an enormously helpful book, and I am recommending it to everyone.
I’ll simply say this about the ongoing debate with the skeptics: the only value I can see in refuting and rebutting these people is to let them know there is a valid and utterly believable alternative to their evolutionary notions. However, that alone will not likely prevail. Resistance to the Bible is a *spiritual* issue, and not a mental or rational one. People cannot see the real reasons they refuse to believe or even consider, and their idea of being fair and unbiased on the issue is easily revealed as a lie. They believe in evolutionism because they want to, plain and simple, and have shown their root cause as refusing to be accountable to their Creator. It is purely a sinner refusing to listen than anything else. As one who has strongly embraced both views, I speak from experience.
I appreciate your exposition. And it’s fairly close to the journey I myself took.
When I decided to let the heart change take effect, I had an advantage that you might not have had. I was taking a post-doctoral fellowship at the time. The faculty of that program included a staunch Christian. This was a fairly small program (run out of one suite of offices, in fact), and no one was going to fire this professor (at least, not then), and more to the point, we saw a lot of each other.
So on the day I told him, “You know this faith you profess? I’m in,” he shared with me a number of articles he had on hand. The World Wide Web was very new in those days, and in fact the Internet had only recently changed its name from Arpanet. So we had Telnet and e-mail and things like that. But he told me where to find certain articles on observations that bore directly on the age of the earth (and the universe).
I need not tell you that those findings flabbergasted me. Things like:
The moon recedes from the earth. (But of course. The tides gradually transfer angular momentum from the earth to the moon.) Were the earth 4.5 billion years old, then at 2.2 billion years Before Present (BP), the moon and the earth should have touched.
The magnetic field weakens with every passing year–slightly, but it adds up in thousands of years. A mere ten thousand years or so ago, that field should have ripped the earth apart.
And of course the uniformitarians never tell you those things. They never tell you that by their own terms, some things set too strict a limit (for their goals) on the age of the earth. Why, shucks! Charles Lyell at first set no limit on the age of the earth. Then Henri Becquerel and the Curies discovered radioactivity. Well, OK, said the evo’s: radioactivity sets a limit on the age of the earth of 4.5 billion years. They could live with that. Or so they thought.
Of course, Dr. Brown lets you know that radioactivity, at least on earth, had its origin in the Flood. And that includes the carbon-14 in the atmosphere. The initial loading came from cluster decay of the newly-formed trans-lead elements. That’s why the patriarchs from Adam to Noah lived 900 years on average. And then the life span of man fell ninety percent, and in eleven generations.
“That’s why the patriarchs from Adam to Noah lived 900 years on average. And then the life span of man fell ninety percent, and in eleven generations.”
Ohhh, that’s what caused the shortened lifespans. All this time I assumed it was due to the increased air pressure caused by the vapor canopy. I know this is in the book, but how did the flood event cause radioactivity to occur?
Your comment about angular momentum transferring to the moon is fascinating. Its exactly that kind of observation that Brown comes up with over and over in his book that challenges and stretches my understanding like virtually nothing I’ve ever encountered. And I really appreciate it, too. That’s why his book has been so helpful.
As I said, I’ve been a Christian now for 27 years, and have two significant periods of declension – the first happened two years in, and cost me 3 years of backsliding, whereas the last happened 11 years ago, and cost me 10 in uselessness. After both periods, God has been revealing things to me that I literally had no idea about. I’m astounded, (because I’m a fairly astute guy and like to look into these things.)
That I had never heard of hydroplate before a few months ago is a revelation, and I believe God withheld it from me for this exact reason – so I appreciate that what I know comes from Him, is a gift, and is meant to be received with thanksgiving and shared with others in the same vein. “Why dost thou glory, as if thou hadst not received [it]?” or, Why do you behave like what you now know didn’t come as a gift?
I tend to trust Dr. Brown quite a bit in these matters, as his scientific understandings are vastly more astute than mine. He has raised issues with my understanding that make feel like I know virtually nothing at all.
One thing I strongly desire is a visualization of these events as they are described. Its very hard for me to imagine how the hydroplates shifted as they did, causing buckling in the Pacific, and mountain ranges upon some continents. Also, the timing of the receding waters carving canyons at the bottom of what is now the Pacific is likewise hard to visualize. I’ve watched as many YT videos as I can. Does Dr. Brown have any others?
Questions, questions. Many questions I have, but I have to finish reading the book first, because I know many of them are already there.
The flood event, as Dr. Brown explains in his book, provoked earthquakes the like of which no human, after the Flood, has ever felt. I personally estimate magnitude 10 to 12. Those quakes began at what became the Mid-Atlantic Ridge. The flood began when a subcrustal ocean broke confinement and shot out in a hypersonic jet along that line. That jet caused the edges of the crust to flutter – and you can imagine what kind of earthquake that involves.
Now one of the most abundant constituents of the crust is quartz. Quartz is a peculiar mineral. Stretch or squeeze it, and you create electromotive force (the quantity we measure in “volts”). Now imagine how many volts a magnitude-10 earthquake can produce with all that quartz. Enough to turn other minerals into atomic plasma. Plasma can fuse, even if the atoms involved are heavier than iron. That is the source of every heavier-than-lead element you can find in the earth’s crust today. Dr. Brown says the transmutation went at least as high as uranium, and maybe to plutonium. (The Oklo formation, today, produces plutonium. It is also the hottest spot on earth for lightning strikes. And lightning is powerful enough to produce plasma along its path.)
Dr. Brown has not produced any more videos, as far as I can tell. But you might play this video by someone who noticed that a formation made three years before, turns out to be stratified. it provides evidence that you don’t need millions of years to lay down the layers of the “geological column.”
That’s amazing, and is what I mean when I say Dr. Brown has taken these conclusions so much farther down the road than any comparable creation scientist. It really involves having a deep and overall awareness of so many physical properties and considerations, and then continuing along a logical path of considerations. I don’t know many people who have that kind of awareness, (which is why the argument is so weak that the lack of a professional degree in any given area necessarily disqualifies from drawing conclusions or inferences.)
Is the core of the Earth molten? If so, how do we know? I thought seismic samples could only penetrate but so far. Seems like the notion is purely an evolutionary one, and that the heat under the earth comes from latent friction of the sliding hydroplates.
Well, actually, the inner core of the earth is not molten, but the inner core swims in an outer core that is molten. You see, the temperature is high enough to melt most metals, but not all.
More to the point: how did the earth’s core get molten? Not from accretion, as the nebula theory would have you believe. But it got molten from gravitational settling. And you have friction at the Bonhoff fault planes near the trenches. (Those are not “subduction zones.” They are, however, zones of friction.”)
So the Earth’s core is molten but it did not form that way. It got that way from gravitational settling and stays that way from insulation and friction. And it certainly did not get that way from radioactive decay.
How are the inner layers of the earth examined, Terry? How deep have seismic soundings actually penetrated, (or what do they use to get down so deep?)
Many things get reexamined, once you start asking questions. Remember the Peruvian Miners trapped a couple years ago? How the story was it was so hot down there. Hot? I thought the lower you went, the cooler it got. So where does the heat come from.
Now I understand it – that heat is latent from the flood, and has been trapped there aprox 4k years, (which is fascinating to think about.)
Is this temperature changing – getting hotter or cooler? Does that have an effect on determining its age?
Correct. The heat is latent from the Flood. Specifically, the crust broke up into several plates, which moved on what was left of the subcrustal ocean before almost all of it flowed out. (The Black Smokers of the Mid-Atlantic Ridge are all that remains of the supercritical water of that ocean.) When those plates settled, and in fact crashed into the old subcrustal ocean floor (or into one another), all that energy had to go somewhere. It released as heat.
The present temperature of the earth’s core probably cannot definitely “date” the earth. But it can suffice to show that the earth cannot be as old as 4.5 billion years. Here’s why: if the earth began as a molten ball, it would have cooled to its present condition in far less time than the 4.5 billion years that most radiometric dating methods seem to suggest.
These technical notes show the details of Dr. Brown’s calculations of the heat of gravitational settling and other considerations about geothermal heat.
Do they know the water coming out of the black smokers is supercritical? (Never had heard of that term before this study.) If so, that would be fairly strong evidence of the hydroplate.
Another issue I’m working with is the thickness of the crust, being 10 miles deep. Hard to imagine 3/4 miles of water being enough lubrication upon which to slide those plate. Always seemed to me the crust should be thinner and the water cavity thicker. If the plates buckled and thickened as they moved into each other, it just seems that 3/4 mile thick chamber is not enough height to produce the depth of the Pacific ocean trenches. Does that make sense?
The water lubricated the plates just enough to make them slide as they did. All the sliding occurred within the Flood year. Dr. Brown worked it out – in full.
“Hard to imagine 3/4 miles of water being enough lubrication upon which to slide those plate.”
Actually, if the hydroplate story had any validity at all an inch of water would be adequate lubrication.
Are you by any chance a parodist?
“if the earth began as a molten ball, it would have cooled to its present condition in far less time than the 4.5 billion years that most radiometric dating methods seem to suggest.”
You’re forgetting about radioactivity. You’re in good company with that particular error though; so did Lord Kelvin.
Now you know that Dr. Brown has an answer to that. Radioactivity is a consequence of the Flood, and has contributed nothing to warming the core.
What makes you think it has no validity at all?